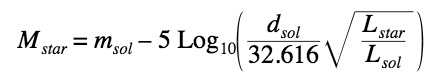how to calculate magnitudes?

[t00fri]

Indeed, my equation could be simplified considerably. Sorry, I didn't took time to write it correctly. Here it is, but I can't confirm your equation was right, as I don't know the magnitude definition.



What is this damn number, 32.616 anywway ? Equations should always be writen in an unit independant way. Is this related to distance in parsecs ? I hate parsecs to death.

Indeed this number 32.616 is "dangerous", since it implicitly carries the dimension of light years! So if one inserts some value for d_star, that value has to be converted to ly first. I did not control that number however (yet). It's 2 o'clock in the morning over here

Bye Fridger

[Evil Dr Ganymede]

Gah! Still the result is the same - if Lstar/Lsol = 1, and d_star = 1.5844e-5 ly (1 AU), then M_star = 36.4, which is wrong.

The Absolute Magnitude of the sun should be -26.74. I can get that by replacing the - sign in Cham's equation with a + sign.

But if I keep Lstar/Lsol = 1, and change d_star, this number changes. Why? If it really is the magnitude of the star at 10 parsecs, then it shouldn't change at all! And also, if I keep the distance the same and increase the luminosity of the star, the Absolute Magnitude goes closer to 0 - i.e the star get dimmer?! That makes no sense. So it doesn't look like swapping the sign makes any sense at all.

See, this isn't so simple or straightforward at all...

[Cham]

Evil, you should get everything there :

http://www.physicsdaily.com/physics/Absolute_magnitude

In my formula, I don't think the d_sol is right. Should be d_star, I think. But I based my formula on the one you gave in another post.

And don't forget this formula is using the base 10 log, NOT the natural log.


Also, that m_sol is weird in the formula. Should be m_star, the APPARENT magnitude of the star, as seen from sol, isn't ?

Should be something like this :

[Evil Dr Ganymede]

Evil, you should get everything there :

http://www.physicsdaily.com/physics/Absolute_magnitude

That's just what Selden quoted earlier though, it doesn't help because it doesn't include the luminosity terms.

And don't forget this formula is using the base 10 log, NOT the natural log.

yep, been using Log10 all along here.

If you watch the star at the distance d_star = 10 parsecs = 32.6 LY, AND the star has the same L as our sun, then you get Log(1) = 0 and M = m.

That is what should be happening... Hm. That does work in your simplified equation. Odd.

So why the hell does that work, when I get a result of M = 36.4 when I set L_star/L_sol = 1 and d_star = 1 AU (1/63115.2)? Am I using the right number for d_star there?!

I suspect that radical(L/L) in the formula isn't right.

There's definitely something wacky going on here. Either I'm not using a right number for one of the constants, or there's something wrong with the equation itself.

[Cham]

Evil, read again my previous post, I've edited it.

Now, I have to go. Later maybe, I'll make some calculation to get the right formula. I don't think this is hard to do.

Later.

[Evil Dr Ganymede]

Also, that m_sol is weird in the formula. Should be m_star, the APPARENT magnitude of the star, as seen from sol, isn't ?

Should be something like this :

Don't think so. The whole point is that we don't know the apparent or absolute magnitudes of the star. All we know is the Luminosity of the star and how far it is from us (and the apparent magnitude of the sun).

Hey, wait a minute. m_sol is the APPARENT magnitude of the sun, right? Which is -26.74, not 4.83 (that's the ABSOLUTE magnitude). I've been getting them the wrong way round!! (See, I told you I make stupid mistakes).


OK, so now if I put that into your equation here:



and use L_star/L_sol = 1 and d_star = 1.5844e-5 ly, then I get M_star of 4.83, which is correct.

But there is still a problem - if I keep the luminosity = 1 and increase the value of d_star (so it's further away from us), the M_star value DECREASES, which doesn't make any sense. Why should the magnitude of the star if placed at 10 pc change at all if the luminosity is not being changed?

(here's the formula I'm using in Excel if you want to check it:

Code: Select all

-26.74 - 5*LOG10((B2/32.616)*SQRT(A2))

Where B2 = d_star, and A2 = L_star/L_sol. It should be the same as Cham's equation 2.

[julesstoop]

[not of any help]
Interesting read. It seems you are somewhat like me: good with concepts and visualisation but an algebraic disaster ;)
Anyhow. As I was coming to the last post I was about to point out that you most probably swapped the apparent and the absolute magnitude.
[/not of any help]

[Evil Dr Ganymede]

OK, I think I got it.

My first equation was actually correct, but I'd swapped the absolute and apparent magnitudes for Sol around. The following appears to be correct:

Equation for calculating Absolute Magnitude of a star given only its Luminosity and Distance from viewer.


Possibly this equation can be simplified, but I'm not going to try it . Given that the distance seems to be irrelevant, that surely has to cancel out somehow.

I get a value of M = 4.83 for a star with L = 1 and d_star = 1.5844e-5. This stays the same regardless of distance (which is as it should be).

If I increase the luminosity to L = 50 (Vega), this means that M = 0.58, which agrees with what Celestia claims is the Absolute Magnitude of Vega (I'm using the luminosity for Vega given in Celestia too)

This seems to work for other stars too, so the equation I'm posting here is most likely to be correct (unless anyone can see otherwise?).


Now that I know M, I can now use:

Code: Select all

m = M + 5*log10(d/32.616)

To figure out what the APPARENT magnitude of the star would be from the planet, right?

[Cham]

Possibly this equation can be simplified, but I'm not going to try it . Given that the distance seems to be irrelevant, that surely has to cancel out somehow.

I get a value of M = 4.83 for a star with L = 1 and d_star = 1.5844e-5. This stays the same regardless of distance (which is as it should be).

Evil, your equation is EXACTLY the same as the one I wrote. The star distance disapears completely from your equation, because of the Log property. It's EXACTLY the same as



There is NO d_star in this. And NO m_star either. Apparently, this formula gives an "absolute" magnitude for the star, defined RELATIVE to the apparent magnitude of our sun, and it only depends on the intrinsic luminosity of the star (relative to our sun's luminosity).

[Evil Dr Ganymede]

Hm. Maybe I put a number in wrong then... that's interesting though, because you don't have any (star) terms in there at all other than the luminosity. You could simplify it even further by replacing (d_sol/32.616) with a number (4.858e-7), and (m_sol) with a number too (-26.74). But yes, that definitely works now, so I must have screwed up in transcribing it somehow...

I managed to persuade Maple to simplify the equation I posted though. Except for some odd reason it doesn't like Logs and insists on converting everything into Ln... but it seems to be the same thing, just a lot simpler:

Code: Select all

M_star = 4.83 - [1.086* ln(L/d^2)] - [2.17*ln(d)]


Yes, it looks very different, but it gives the same results (and I'm not going to doubt Maple). Though it's weird that the -26.74 value (the apparent magnitude of Sol) is replaced by 4.83 (which happens to be the absolute magnitude of Sol). I don't think that's coincidence...

That's definitely more digestible anyway .

I checked the apparent magnitude formula too, that works fine with these values. Huzzah! (thanks for all the help everyone!)

[Cham]

I think I now understand the physics behind all this. It's not so complicated finally. Unfortunately, I'm not home right now, and I can't use my tools to write nice equations here. So I'm forced to write them in "ascii". Here it is.

Let the "intensity" of light, emited by the star and received at the Earth location, be "I". And let the intrinsic power of the star be "P" (I'm pretty sure this is the same as "L" for luminosity). Then we have the well known formula, which is a consequence of the DEFINITION of the intensity (I = P/Aera) :


I = P/4Pi d^2.


This is a relation between physical quantities. P is measured in "watts" (or "joules per second"). I is measured in watt per meter-squared.

Now, in the same fashion as the acoustic level definition ( which is Beta = 10 dB Log(I/I_0) ), we DEFINE the star MAGNITUDE with a log formula :


m = A Log( B I ) + C


where A, B and C are ARBITRARY constants. This "m" isn't a physical quantity and is just a convention, a mere definition. Now, to have a sensible relation which makes sense, we can only make comparisons with something else. We need to define the magnitude RELATIVE to something else. So we select our sun at d = 1 AU. The APPARENT magnitude of the star is then DEFINED as


Delta m = m_star - m_sol .


Now, using the Log properties, this definition gives


m_star = m_sol + A Log( B I_star ) - A Log( B I_sol )

== m_sol + A Log( I_star / I_sol ).


Now, using the defintion of the intensity I above, this gives


m_star = m_sol + 2A Log[ ( d_sol / d_star ) Sqrt( P_star / P_sol ) ]


Recall that the constant A is arbitrary. Astronomers have selected 2A = -5. Let me be clear. This formula gives a definition of the APPARENT MAGNITUDE, and clearly depends on the star's intrinsic power AND on its distance. This makes physical sense. Now, we DEFINE the ABSOLUTE MAGNITUDE as the magnitude of the star located at d_star = 10 parsecs = 32.616 LY (convention). This gives finally the formula


M_star = m_sol - 5 Log[ ( d_sol / 32.616 ) Sqrt( P_star / P_sol ) ]


which is exactly the formula I pasted earlier :




Recall that here, d_sol is really 1 AU. The absolute magnitude does not depend on the star's distance, which makes sense.

[t00fri]

which is exactly the formula I pasted earlier :




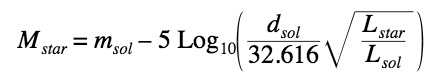
Recall that here, d_sol is really 1 AU. The absolute magnitude does not depend on the star's distance, which makes sense.

That formula is not only correct it also makes obviously sense! Why? OK, let's consider two implications of it:

a) We may identify 'star'='sol' then we get immediately:

Code: Select all

M_sol = m_sol -5*log10(d_sol [ly]/32.616)


since the ratio L_star/L_sol =1 for that special case.
Remembering that in this formula d_sol is to be inserted in ly, we may rewrite it also, using 32.616 ly = 10 pc as

Code: Select all

M_sol = m_sol - 5*log10(d_sol [pc]/10)


This simple check shows that the above formula was correct, since for the special case 'star'='sol' it boils down to one of our two starting equations!

b) Next we may subtract the latter equation (for 'star'='sol') from the more general one (with 'star' <> 'sol' ). Then the apparent magnitude m_sol of 'Sol' cancels and we get right away:

Code: Select all

M_star -M_sol = 5/2*log10(L_sol/L_star)


This is clearly the simplest version of the M <-> log L
relation. We may now insert some numbers to get a feel...

m_sol = - 26.73
d_sun = 1.58 x10-5 ly = 4.844x10-6 pc
hence
M_sol = - 26.73 - 5*log10(4.844x10-6/10) = 4.84 => OK

If we want to express the star's luminosity in Watts, we may use

L_sol = 3.827?—10^26 W

and our above formula becomes

Code: Select all

M_star =4.84 - 5/2*log10(L_star [W]/3.827x10^26)


There is a completely analogous equation, involving the apparent magnitude differences on the l.h.s and instead of the log10 of the Luminosity ratio, now the log 10 of the flux ratio appears on the r.h.s.

To get the radiation flux f from the luminosity L (radiated energy), we have to divide L by the illuminated area at distance d from the light source, ( flux= enery/area, dimensionally), i.e

Code: Select all

f = L/(4*Pi*d^2)


I guess Cham wrote that formula also earlier above.

We then get instead:

Code: Select all

m_star - m_sol = 5/2*log10 (f_sol/f_star)


You certainly notice the similarity with the above formula for the difference of absolute magnitudes.

+++++++++++++++++++
The luminosity L characterizes the radiation output of a star and thus is a constant independent of the distance from that star. So is the absolute magnitude being essentially ~log(L).

The apparent magnitude or (equivalently) the radiation flux depends on the distance according to the familiar inverse square law.
+++++++++++++++++++

Bye Fridger

[Evil Dr Ganymede]

Thanks everyone, I've now got about 5 or 6 different equations that all mean the same thing and give the same results .

I've also found that m = 6 is about the limit that can be detected by the naked eye on a good night, m = -4 is about the minimum you need to cast shadows with... Does anyone have any idea what kind of apparent magnitude would be required to 'turn night into day' (i.e. scatter light in the atmosphere enough to get noticeably blue sky)? I'm figuring it must be something between -12 (full moon) and -26 (sun) - can anyone pin it down further?

[julesstoop]

I know for one that a sun that's been eclipsed for 98% (a difference of 3 to 4 manitudes compared to a 'full' sun) doesn't turn day into night. The light gets a little strange, but the sky definitely remains blue.
So it must be above -23 and below -12

[ArneB]

He, he, I was just reading this post, and the first page reminded me of a Larson cartoon; A bunch of scientists are doing typical science stuff (conducting experiments and solving equations) when the ice-cream truck arrives, and total mayhem breaks out.

[Evil Dr Ganymede]

Question about Planet magnitudes:
referring to http://www.answers.com/topic/absolute-magnitude

In this case, the absolute magnitude is defined as the apparent magnitude that the object would have if it were one astronomical unit (au) from both the Sun and the Earth and at a phase angle of zero degrees. This is a physical impossibility, but it is convenient for purposes of calculation.

1) Isn't this just the same as saying "this is the apparent magnitude the object would have if you were looking at it directly from the surface of the sun with it placed at a distance of 1 AU and at a phase angle of zero degrees"? (ie it is directly overhead)


2) In the formulae for absolute planet magnitude, should you replace m_sun with m_star if the star in question is not the sun? That would seem to make sense to me...