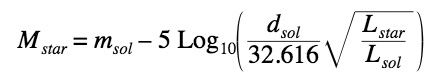Cham wrote:which is exactly the formula I pasted earlier :
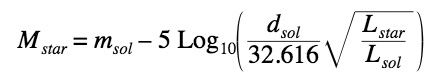
Recall that here, d_sol is really 1 AU. The absolute magnitude does not depend on the star's distance, which makes sense.
That formula is not only correct

it also makes obviously sense! Why? OK, let's consider two implications of it:
a) We may identify 'star'='sol' then we get immediately:
Code: Select all
M_sol = m_sol -5*log10(d_sol [ly]/32.616)
since the ratio L_star/L_sol =1 for that special case.
Remembering that in this formula d_sol is to be inserted in ly, we may rewrite it also, using 32.616 ly = 10 pc as
Code: Select all
M_sol = m_sol - 5*log10(d_sol [pc]/10)
This simple check shows that the above formula was correct, since for the special case 'star'='sol' it boils down to one of our two starting equations!
b) Next we may subtract the latter equation (for 'star'='sol') from the more general one (with 'star' <> 'sol' ). Then the apparent magnitude m_sol of 'Sol' cancels and we get right away:
Code: Select all
M_star -M_sol = 5/2*log10(L_sol/L_star)
This is clearly the simplest version of the M <-> log L
relation. We may now insert some numbers to get a feel...
m_sol = - 26.73
d_sun = 1.58 x10-5 ly = 4.844x10-6 pc
hence
M_sol = - 26.73 - 5*log10(4.844x10-6/10) = 4.84 => OK
If we want to express the star's luminosity in Watts, we may use
L_sol = 3.827?—10^26 W
and our above formula becomes
Code: Select all
M_star =4.84 - 5/2*log10(L_star [W]/3.827x10^26)
There is a completely analogous equation, involving the
apparent magnitude differences on the l.h.s and instead of the log10 of the Luminosity ratio, now the log 10 of the
flux ratio appears on the r.h.s.
To get the
radiation flux f from the luminosity L (radiated energy), we have to divide L by the illuminated area at distance d from the light source, ( flux= enery/area, dimensionally), i.e
I guess Cham wrote that formula also earlier above.
We then get instead:
Code: Select all
m_star - m_sol = 5/2*log10 (f_sol/f_star)
You certainly notice the similarity with the above formula for the difference of absolute magnitudes.
+++++++++++++++++++
The luminosity L characterizes the radiation output of a star and thus is a
constant independent of the distance from that star. So is the
absolute magnitude being essentially ~log(L).
The
apparent magnitude or (equivalently) the radiation flux depends on the distance according to the familiar inverse square law.
+++++++++++++++++++
Bye Fridger