With this line
Code: Select all
float d_vis = (14.8f + 86.9f * effSize) * (float)
being from my least-square fit (MAPLE) of a
linear dependence, d_vis = a + b * I, to a vector of importance weights (I) along with the corresponding minimal distances (d_vis(I)), where the locations with these importance weights just become visible.
DW specialized to importance weights being effective
location sizes.
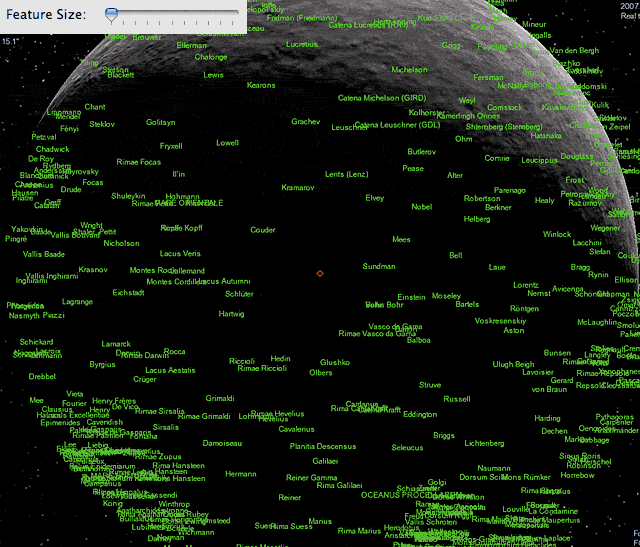
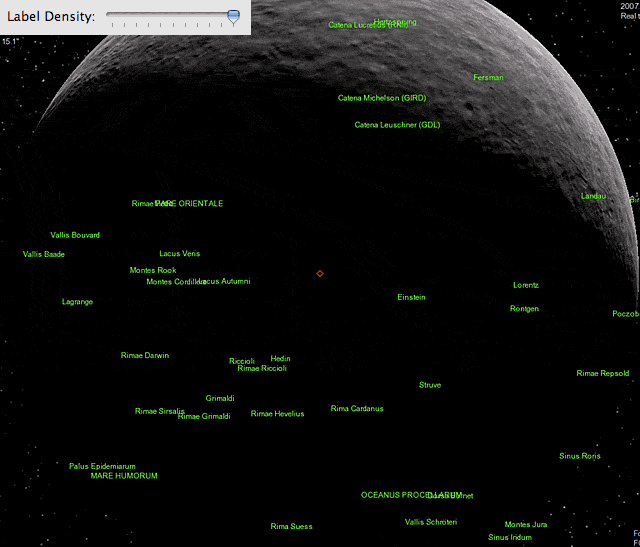
Here is the result of my previous analysis, comparing the fit d_vis = 14.8 + 86.9 * (importance weight) to the actual "data" points for the case of my 1600x1200 monitor.

The threshold distances at which locations with a given importance weight just became visible were determined empirically and cross-checks for lower monitor resolutions were also done.
The shown results and above parameters are several years old. My commented analysis can be studied in detail e.g. in these published Maple worksheets.
Moon:
http://www.celestiaproject.net/~t00fri/images/moon_weights.pdf
Earth:
http://www.celestiaproject.net/~t00fri/earth.html
to be found in various posts of mine in the forum.
At the end of the day, my analysis depends only on
ONE parameter to be adjusted according to gusto:
it determines the number of labels visible at a certain reference distance. That parameter you can adjust with the above slider, as nicely illustrated in DW's images.
Bye Fridger