About the Orientation command

[Cham]

I'm puzzled about the Orientation command in SSC files and I need a confirmation of what I've found. I'm guessing only Chris, Fridger or Selden have the answer to the following question (of course, I may be wrong).

Until today, I believed that I could only apply a single rotation with only the value "1" as the rotation axis in the Orientation command, like these examples below :

Orientation [90 1 0 0] (90?° rotation around the "x" axis)
or
Orientation [90 0 1 0] (90?° rotation around the "y" axis)
or
Orientation [90 0 0 1] (90?° rotation around the "z" axis)
or
Orientation [90 1 1 0] (90?° rotation around what direction ???)
etc.

To make sense, the last three numbers should be the components of an unit vector (the axis of rotation). So [90 1 1 1] for example doesn't make much sense to me. Is it equivalent to the unit vector (1, 1, 1)/sqrt(3) (properly normalised) ?

So are we allowed to use non-integer values (possibly negative) in the last entries of the Orientation command, like this below ?

Orientation [90 0.93969 -0.34202 0]

I tried, and apparently it worked. But I still need a confirmation.

[selden]

The Orientation declaration uses what is known as the Axis,Angle convention for specifying how a body is, well, oriented.

http://en.wikipedia.org/wiki/Axis_angle
describes how they are defined. Essentially the 3 Axis values describe where the model's axis points and the Angle describes its rotational orientation around that axis.

Each of the 3 Axis values can have any value between 0 and 1, but they have to be normalized to 1. That is, the square root of the sum of their squares = 1. (i.e. they form a unit vector.)

The actual relationship between the Axis values and a direction in Celestia or for the model is not something I've been able to keep straight. At one point I thought I understood it, but after doing things with the Lua Scripted functions, I'm now thoroughly confused.

[mjoubert]

Cham,

The vector used to define orientation is normalized, so you don't have to worry about that.

As it's a bit tricky to use "Orientation" and obtain rotation you expect (orientation is computed in Celestia reference frame), we made here an helper : it displays all of the 24 positions of a die.

You can check this picture to see the rotation applyed to a colored cube : if you don't apply any orientation, you'll got the cube in the top left corner. For exemple, if you apply [180 0 1 1] (column 3, row 4 in the array), you'll obtain the corresponding yellow front face cube (col 3, raw 4).

Hope it helps.

Mathieu (spacebel)

[mjoubert]

And note that there a several orientations that lead to a same position

So [270 0 0 -1] (col 1 row 4), is equal to [90 0 0 1].

Mathieu

[Cham]

Thanks for the replies, guys.

Selden, so you're confirming that the following command is allowed ?

Orientation [30 0.93969 0.34202 0]

Each of the 3 Axis values can have any value between 0 and 1, but they have to be normalized to 1. That is, the square root of the sum of their squares = 1. (i.e. they form a unit vector.)

And what about negative values ?

Then since we can't enter the exact (irrational) values, how Celestia knows that the vector is normalised ? I mean, can I give approximate values like these ?

Orientation [30 0.94 0.34 0], or even Orientation [30 0.9 0.3 0]

The vector isn't well normalised, in this case ! And then, why can't I put values like these ?

Orientation [30 0.5 0.5 1]

[selden]

Cham,

Sorry, I probably should have written that the absolute values of the individual numbers should be less than one: since it's a unit vector in 3D space, any of them can be negative.

Of course, since the calculations are being done on a computer, normalization is approximate.

While Celestia may very well perform the normalization itself in this case, I've seen the warning "values must be normalized" in too many places to be able to remember when it's not necessary, and it's easy enough to do, so...

[Cham]

Thanks Selden.

Then, any normalised values are allowed in this command. For such a long time, I was believing that only "1" was allowed, and nothing else !

[Cham]

Here are specific examples of the Orientation command effects.

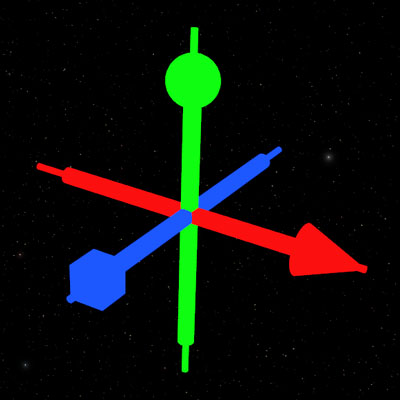
Here's the original *FIXED* axis and an aligned model. The "heads" are indicating the positive directions in my modeler :



Here's a 90?° rotation around the "x" axis (Orientation [90 1 0 0]) :

[img]http://nho.ohn.free.fr/celestia/Cham/Divers/[90-100].jpg[/img]

Here's a 90?° rotation around the "y" axis (Orientation [90 0 1 0]) :

[img]http://nho.ohn.free.fr/celestia/Cham/Divers/[90-010].jpg[/img]

Here's a 90?° rotation around the "z" axis (Orientation [90 0 0 1]) :

[img]http://nho.ohn.free.fr/celestia/Cham/Divers/[90-001].jpg[/img]

I noticed that the three rotations above are in the reverse sense of the "right hand rule" applied to the axis shown in my modeler. At least, it is consistent.

Here's a 90?° rotation around the "u" = (1, 1, 0) axis (Orientation [90 1 1 0]) :

[img]http://nho.ohn.free.fr/celestia/Cham/Divers/[90-110].jpg[/img]

I explicitly verified that the (1, 1, 0) values are EQUIVALENT to the normalised axis (1, 1, 0)/sqrt(2), so

Orientation [90 1 1 0] == Orientation [90 0.7071 0.7071 0]