And Celestia can't as yet tell me the apparent magnitudes of planets or moons. Is there a way to figure this out by hand (I'm assuming it has to do with the luminosity of the star and the albedo of the planet?)
how to calculate magnitudes?
-
Topic authorEvil Dr Ganymede
- Posts: 1386
- Joined: 06.06.2003
- With us: 21 years 8 months
how to calculate magnitudes?
How does Celestia figure out the apparent and absolute magnitudes of stars? Sometimes I have to figure out how bright a companion star is as seen from the surface of a planet orbiting the primary - I use Celestia to give me a quick answer, but I'd still like to know how it calculates them  .
.
And Celestia can't as yet tell me the apparent magnitudes of planets or moons. Is there a way to figure this out by hand (I'm assuming it has to do with the luminosity of the star and the albedo of the planet?)
And Celestia can't as yet tell me the apparent magnitudes of planets or moons. Is there a way to figure this out by hand (I'm assuming it has to do with the luminosity of the star and the albedo of the planet?)
- t00fri
- Developer
- Posts: 8772
- Joined: 29.03.2002
- Age: 22
- With us: 22 years 10 months
- Location: Hamburg, Germany
Re: how to calculate magnitudes?
Evil Dr Ganymede wrote:How does Celestia figure out the apparent and absolute magnitudes of stars? Sometimes I have to figure out how bright a companion star is as seen from the surface of a planet orbiting the primary - I use Celestia to give me a quick answer, but I'd still like to know how it calculates them.
And Celestia can't as yet tell me the apparent magnitudes of planets or moons. Is there a way to figure this out by hand (I'm assuming it has to do with the luminosity of the star and the albedo of the planet?)
for stars, Celestia uses the apparent (visual) magnitudes as tabulated in the HIPPARCOS catalog.
From there one may compute the absolute luminosity (and hence the absolute magnitude) in units of the known solar luminosity, provided one knows the star's distance:
Code: Select all
L_star/L_sol = (d_star/d_sol)^2*10^(0.4*(m_sol - m_star))
with d_sol ~ 1.58e-5 ly, m_sol=-26.73
If one is interested in the star's /total/ luminosity (i.e. the total energy radiated into space including all wave lengths), one should incorporate the bolometric correction in addition.
You find all these formulae in any respective textbook or many times on the web...Writing formulae here is just too tedious and time consuming.
Last edited by t00fri on 28.05.2005, 09:32, edited 1 time in total.
-
Topic authorEvil Dr Ganymede
- Posts: 1386
- Joined: 06.06.2003
- With us: 21 years 8 months
- t00fri
- Developer
- Posts: 8772
- Joined: 29.03.2002
- Age: 22
- With us: 22 years 10 months
- Location: Hamburg, Germany
Evil Dr Ganymede wrote:So magnitude is an entirely relative scale? i.e. it's all referenced to the magnitude of the sun?
Not at all. The absolute magnitude/luminosity has a general definition that is independent of any other body. Yet /in practice/ it's better or convenient to relate it to the sun's well known luminosity. As a reminder: The absolute magnitude is essentially the logarithm of the luminosity.
Last edited by t00fri on 28.05.2005, 09:34, edited 1 time in total.
-
Topic authorEvil Dr Ganymede
- Posts: 1386
- Joined: 06.06.2003
- With us: 21 years 8 months
Hm, well absolute magnitude may be useful (I'm very rusty on this, in case you haven't noticed).
So if Abs Mag is how bright the object is if it's placed at a distance of 10 pc from the viewer, then how is that calculated? I've scoured websites looking for this and I can't find a decently explained no-nonsense formula that shows the relationship between (Visible) Luminosity and Absolute Magnitude. (assume that I know the luminosity of the star).
So if Abs Mag is how bright the object is if it's placed at a distance of 10 pc from the viewer, then how is that calculated? I've scoured websites looking for this and I can't find a decently explained no-nonsense formula that shows the relationship between (Visible) Luminosity and Absolute Magnitude. (assume that I know the luminosity of the star).
Oh Evil One,
A star's absolute magnitude usually is calculated from its apparent magnitude, which can be measured.
See http://www.answers.com/topic/absolute-magnitude
It includes some worked examples.
A star's absolute magnitude usually is calculated from its apparent magnitude, which can be measured.
See http://www.answers.com/topic/absolute-magnitude
It includes some worked examples.
Selden
- t00fri
- Developer
- Posts: 8772
- Joined: 29.03.2002
- Age: 22
- With us: 22 years 10 months
- Location: Hamburg, Germany
Evil Dr Ganymede wrote:Hm, well absolute magnitude may be useful (I'm very rusty on this, in case you haven't noticed).
So if Abs Mag is how bright the object is if it's placed at a distance of 10 pc from the viewer, then how is that calculated? I've scoured websites looking for this and I can't find a decently explained no-nonsense formula that shows the relationship between (Visible) Luminosity and Absolute Magnitude. (assume that I know the luminosity of the star).
+++++++++++++++++
The absolute magnitude M of a star is generally defined as its apparent magnitude m at a distance of 10 Parsecs.
+++++++++++++++++
This implies various immediate ways of calculation:
a) In terms of the star's apparent magnitude m measured e.g. on Earth (distance d in parsec from the star):
Code: Select all
M = m - 5*log10(d/10pc)
b) In terms of the star's luminosity L:
Use the formula in my previous post above and express L <-> M via a) . I am too lazy. Anyhow M ~ log L as I said above.
For planets, comets & asteroids a different definition of "absolute magnitude" is used:
In this case, the absolute magnitude H is defined as the apparent magnitude that the object would have if it were one 1 AU from both the Sun and the Earth and at a phase angle of zero degrees. This is a physical impossibility, but it is convenient for purposes of calculation
Code: Select all
H_body = m_sun-2.5*log10(a_body*d_body^2)
m_sun = apparent magnitude of sun at 1 au = -26.73
a_body = geometric albedo of body (between 0 and 1)
d_body = diameter of (spherical) body
Example: Moon
=========
Code: Select all
a_moon = 0.12, d_moon = 3476 km
H_moon ~= 2.5*log10(1329/(0.12*3476^2)) = +0.21
Similarly one can also introduce the apparent magnitude of a planet, but I am getting tired of writing. These formulae are really to be found in every textbook.
-
Topic authorEvil Dr Ganymede
- Posts: 1386
- Joined: 06.06.2003
- With us: 21 years 8 months
Ack. This is getting circular.
So you're saying that in order to find the absolute magnitude of an object (which is far more useful than the apparent magnitude for my purposes), I have to first figure out its apparent magnitude, but that's only determined by observation? (which is not useful, since I want to calculate it based on the luminosity and distance alone, not on apparent magnitudes. Which surely must be possible to do).
Fridger hints at formulae that can figure out the proper relation between absolute magnitude and luminosity and then doesn't bother to elaborate on them much, but I don't have them and I can't find them anywhere. With all due respect, I don't want lazy, half-written answers. I would like someone to either explain - fully - how this works and not miss out steps or expect me to know how to rearrange the equations myself or assume that I know things, or I would like to be pointed to a website that explicitly and clearly explains how to calculate Absolute Magnitude directly from Luminosity. I wouldn't be asking here if I didn't know how to do it or couldn't find it myself.
As it is, the relationship of M ~ log L doesn't seem to hold. If I use L = 1, then that means M = 0 (it should be about 5 for Sol). If I use log of Sol's luminosity in watts (about 3.8e26) then I get a value of 26. This evidently is not accurate without more information.
The best I can get is:
but since I don't have m or M, this isn't much use unless I have a way to express m and/or M in terms of the Luminosity of the star. Plus, if I put values for Sol into that (m=+4.83, M=-26.73) then I get d/10pc = 10^6.312 = 2051162, which makes no sense. Have I done something wrong here? (and yet, if I try for Rigel, with m = 0.18 and M = -6.7, I get d/10pc = 23.77, so d = 774.8 lightyears which is about right. And I get the right answer for Vega too (about 25 lightyears away) using its values for m (0.03) and M (0.65). So why do I get such a huge value for the sun?)
The information about planet magnitudes at least is on the answers.com link that Selden posted (thanks!). But that still doesn't have how to convert between stellar luminosity and absolute magnitude.
So you're saying that in order to find the absolute magnitude of an object (which is far more useful than the apparent magnitude for my purposes), I have to first figure out its apparent magnitude, but that's only determined by observation? (which is not useful, since I want to calculate it based on the luminosity and distance alone, not on apparent magnitudes. Which surely must be possible to do).
Fridger hints at formulae that can figure out the proper relation between absolute magnitude and luminosity and then doesn't bother to elaborate on them much, but I don't have them and I can't find them anywhere. With all due respect, I don't want lazy, half-written answers. I would like someone to either explain - fully - how this works and not miss out steps or expect me to know how to rearrange the equations myself or assume that I know things, or I would like to be pointed to a website that explicitly and clearly explains how to calculate Absolute Magnitude directly from Luminosity. I wouldn't be asking here if I didn't know how to do it or couldn't find it myself.
As it is, the relationship of M ~ log L doesn't seem to hold. If I use L = 1, then that means M = 0 (it should be about 5 for Sol). If I use log of Sol's luminosity in watts (about 3.8e26) then I get a value of 26. This evidently is not accurate without more information.
The best I can get is:
Code: Select all
(d/10pc) = 10^[(m-M)/5]but since I don't have m or M, this isn't much use unless I have a way to express m and/or M in terms of the Luminosity of the star. Plus, if I put values for Sol into that (m=+4.83, M=-26.73) then I get d/10pc = 10^6.312 = 2051162, which makes no sense. Have I done something wrong here? (and yet, if I try for Rigel, with m = 0.18 and M = -6.7, I get d/10pc = 23.77, so d = 774.8 lightyears which is about right. And I get the right answer for Vega too (about 25 lightyears away) using its values for m (0.03) and M (0.65). So why do I get such a huge value for the sun?)
The information about planet magnitudes at least is on the answers.com link that Selden posted (thanks!). But that still doesn't have how to convert between stellar luminosity and absolute magnitude.
- t00fri
- Developer
- Posts: 8772
- Joined: 29.03.2002
- Age: 22
- With us: 22 years 10 months
- Location: Hamburg, Germany
First of all, please remember that you did not tell anyone here what you wanted to do with the information you were asking for. So it's hard for me and others to become more specific.
I just figured that people with a PhD in science should be able to combine two simple equations for themselves correctly. The 1st equation I was referring to above was
i.e expressing the star's luminosity L_star in terms of the apparent magnitude m_star (given the known solar luminosity and apparent solar magnitude).
The second equation I asked you to use was
So you solve the latter for m_star and insert it into the equation above. It is so trivial that I feel ashamed to explain it any further, really!
Then you get an expression of L_star as function of M_star.
Taking the logarithm (base 10) of L_star gives an expression linearly proportional to M_star.
Hence log10(L) ~ M_star
precisely as I said. Why should I spend my time working out those straightforward numerical factors for you??
Finally, I made sure that the required information exists also in the Internet in many correct variations. If you like I can give you the search words I used...
But don't worry, you efficiently made me stop writing any further information
I just figured that people with a PhD in science should be able to combine two simple equations for themselves correctly. The 1st equation I was referring to above was
Code: Select all
L_star/L_sol = (d_star/d_sol)^2*10^(0.4*(m_sol-m_star))
i.e expressing the star's luminosity L_star in terms of the apparent magnitude m_star (given the known solar luminosity and apparent solar magnitude).
The second equation I asked you to use was
Code: Select all
M_star = m_star - 5*log10(d_star/10pc)
So you solve the latter for m_star and insert it into the equation above. It is so trivial that I feel ashamed to explain it any further, really!
Then you get an expression of L_star as function of M_star.
Taking the logarithm (base 10) of L_star gives an expression linearly proportional to M_star.
Hence log10(L) ~ M_star
precisely as I said. Why should I spend my time working out those straightforward numerical factors for you??
Finally, I made sure that the required information exists also in the Internet in many correct variations. If you like I can give you the search words I used...
But don't worry, you efficiently made me stop writing any further information
Last edited by t00fri on 28.05.2005, 09:36, edited 1 time in total.
-
Topic authorEvil Dr Ganymede
- Posts: 1386
- Joined: 06.06.2003
- With us: 21 years 8 months
t00fri wrote:First of all, please remember that you did not tell anyone here what you wanted to do with the information you were asking for. So it's hard for me and others to become more specific.
Evil Dr Ganymede wrote:Sometimes I have to figure out how bright a companion star is as seen from the surface of a planet orbiting the primary
...
I've scoured websites looking for this and I can't find a decently explained no-nonsense formula that shows the relationship between (Visible) Luminosity and Absolute Magnitude. (assume that I know the luminosity of the star).
Seems to me that I was very clear about what I wanted to do with the information. I want to be able to figure out how to calculate the Absolute Magnitude and the Apparent Magnitude of a star seen from the surface of a planet, given the luminosity of the star and the distance from the planet.
I just figured that people with a PhD in science should be able to combine two simple equations for themselves correctly.
Would you please just forget that assumption. My mathematical ability is well below that of physicists and astrophysicists - I'm a geologist, and that is what my PhD is in (albeit geology on other planets). Calculus and rearranging equations was never my strong point either.
So you solve the latter for m_star and insert it into the equation above. It is so trivial that I feel ashamed to explain it any further, really!
Why should I spend my time working out those straightforward numerical factors for you??
Jeez, would it kill you to just do that for me? Since you've gone to the trouble of typing that all out (or copying it from whatever hidden webpage you've found that does explain it all), why just stop halfway? You are just being deliberately unhelpful.
I mean, goddammit, Fridger, getting any information out of you is like squeezing blood from a stone.
If people ask for help, it is absolutely pointless for those who are able to help to say "yeah, I know how to do it but I'm not going to bother explaining it so you can understand it". It is also incredibly useless to say "Ok, here's the first step, the rest is obvious" when it isn't that obvious at all. I've had a go at you for that before and evidently you still haven't learned from that. If you don't want to help fully, then don't waste your time by replying at all. It frightens me that you're a teacher sometimes.
As it is, I now have to waste my time figuring out how to put those equations together (and not being sure if I've got it right), when you could have done it much more quickly and I'd be certain of its accuracy.
So you'll forgive me if I'm not falling over myself with gratitude at the scant clues you deign to throw me.
Finally, I made sure that the required information exists also in the Internet in many correct variations. If you like I can give you the search words I used...
Yes, and you didn't bother to point out where to find that information either. Again, a completely useless response from you.
But don't worry, you efficiently made me stop writing any further information
I didn't. You just decided you couldn't be bothered to commit to helping right from the start. You could have just explained everything fully in a single post instead of throwing out disconnected tidbits of information in three or four separate ones. That way you would have answered the questions fully, and I would have actually been grateful for your help, instead of being frustrated at you.
Again, you assume that everyone knows what you know and that everyone has the same capabilities you have. Well, we don't.
Last edited by Evil Dr Ganymede on 27.05.2005, 22:12, edited 1 time in total.
humm, please gentlemen, 
don't start a flame war. It's really not worth it. Relax, drink a beer (or two), and enjoy yourselves.
Et in terra pax, hominibus bonae voluntatis.

don't start a flame war. It's really not worth it. Relax, drink a beer (or two), and enjoy yourselves.
Et in terra pax, hominibus bonae voluntatis.
"Well! I've often seen a cat without a grin", thought Alice; "but a grin without a cat! It's the most curious thing I ever saw in all my life!"
-
ElChristou
- Developer
- Posts: 3776
- Joined: 04.02.2005
- With us: 20 years
-
Topic authorEvil Dr Ganymede
- Posts: 1386
- Joined: 06.06.2003
- With us: 21 years 8 months
I give up. 
Can someone who can do the required mathematical jiggerypokery please just take this equation:
and make M_star the subject of the equation? Please?! Because I'm buggered if I can figure it out. I can't even get a sensible answer out of Maple...
Can someone who can do the required mathematical jiggerypokery please just take this equation:
Code: Select all
(L_star/L_sol) = ((d_star/d_sol)^2) * 10^(0.4*(m_sol-[M_star + 5*log10(d_star/32.616)])
and make M_star the subject of the equation? Please?! Because I'm buggered if I can figure it out. I can't even get a sensible answer out of Maple...
Is that what you need ?

I don't know this formula. I just inverted the equation you gave, to isolate the M_star.
Edit : Oops, I just noticed there's a small typo. You should read 32.616 down there.

I don't know this formula. I just inverted the equation you gave, to isolate the M_star.
Edit : Oops, I just noticed there's a small typo. You should read 32.616 down there.
"Well! I've often seen a cat without a grin", thought Alice; "but a grin without a cat! It's the most curious thing I ever saw in all my life!"
- t00fri
- Developer
- Posts: 8772
- Joined: 29.03.2002
- Age: 22
- With us: 22 years 10 months
- Location: Hamburg, Germany
It frightens me that you're a teacher sometimes.
At least in the part of the world where I live, the general idea is that /teachers/ explain the logical steps of how to arrive at the solution, while the students are gaining practice in working things out explicitly...
I certainly provided all that corresponding information to you. To work out the rest requires simple /high-school/ math NOT the know-how of physicists or mathematicians. In case of planetary magnitudes, I even worked out an explicit numerical example besides the general concepts/definitions, since I thought you were mainly interested in that.
Indeed, after already writing this much, I also intended to work out the final formula for you, but in the very moment, the door bell rang and our visitors for the evening had arrived. That's why I cut it short...
-
Topic authorEvil Dr Ganymede
- Posts: 1386
- Joined: 06.06.2003
- With us: 21 years 8 months
That's what I managed to figure out eventually, but it doesn't look like it's right.
Replacing:
m_sol = 4.83
I got:
Which is almost the same as what you get, but the dsol/dstar is inverted for some reason.
But M_star is the absolute magnitude of the star - ie the magnitude it has if it's placed at 10 pc, right?
So if I set L_star = 1.0, and d_star = 1.58e-5 ly (i.e. I'm putting the Sun at a distance of 1 AU from the Earth), I should get the Absolute Magnitude of the sun, right? Which should be 4.83.
Now, with my version of the formula, I get a value of 36.40. This is the same regardless of the distance (which at least tallies up with it being the Absolute Magnitude - but the number itself is wrong).
If I use Cham's formula, I get 36.39... but that number changes if I change d_star (the distance between earth and the star), so not only is the number itself wrong but it also shouldn't be changing if just the distance to the star is changing.
I should note however, that if I change my equation so that I ADD the 5log... term and SUBTRACT the 1/0.4log... term, I end up with the Apparent Magnitude of the sun (-26.74) for some reason. But then if I change the distance to the star and keep the luminosity of the star at 1, that number changes.
So what the heck is going on?!
Replacing:
m_sol = 4.83
I got:
Code: Select all
Ms = 4.83 - [1/0.4*log((L_star/L_sol)*((d_star/d_sol)^2))] - 5log(d_star/32.616)
Which is almost the same as what you get, but the dsol/dstar is inverted for some reason.
But M_star is the absolute magnitude of the star - ie the magnitude it has if it's placed at 10 pc, right?
So if I set L_star = 1.0, and d_star = 1.58e-5 ly (i.e. I'm putting the Sun at a distance of 1 AU from the Earth), I should get the Absolute Magnitude of the sun, right? Which should be 4.83.
Now, with my version of the formula, I get a value of 36.40. This is the same regardless of the distance (which at least tallies up with it being the Absolute Magnitude - but the number itself is wrong).
If I use Cham's formula, I get 36.39... but that number changes if I change d_star (the distance between earth and the star), so not only is the number itself wrong but it also shouldn't be changing if just the distance to the star is changing.
I should note however, that if I change my equation so that I ADD the 5log... term and SUBTRACT the 1/0.4log... term, I end up with the Apparent Magnitude of the sun (-26.74) for some reason. But then if I change the distance to the star and keep the luminosity of the star at 1, that number changes.
So what the heck is going on?!
-
Topic authorEvil Dr Ganymede
- Posts: 1386
- Joined: 06.06.2003
- With us: 21 years 8 months
t00fri wrote:At least in the part of the world where I live, the general idea is that /teachers/ explain the logical steps of how to arrive at the solution, while the students are gaining practice in working things out explicitly...
Yes, but if it's clear that the student can't figure it out, then you don't just abandon them - you should be explaining it so they DO understand every step. Otherwise they can't learn how to solve the problem.
Let me explain something about me very clearly to you Fridger (and to everyone else), and then maybe you might understand - my numerical abilities are way below the usual standard that you might expect from a scientist. I am very good with concepts and visualisation and most of the other aspects of scientific thinking, but I am very bad at brute force number-crunching and mathematical fiddling. I can't even do simple mental arithmetic without either taking a long time over it or making a stupid mistake somewhere along the line. I certainly can't rearrange a complex equation and figure out if I've done it right either without actually plugging in some numbers (and as far as I can tell given my previous post, I HAVE done it right and yet the results are still making no sense).
I'm sure that given that it may boggle you that I have a PhD - it amazes me sometimes, believe me. My PhD was not heavily mathematical, though there were parts of it where it was necessary so I had to get my supervisor to sort out the equations because I sure as hell couldn't do them myself. I simply don't have the aptitude for that sort of thing. I came up with the ideas and the original concepts and explained them, and I programmed and ran models and in the end I successfully defended my work. Now, I don't care what you think of that, but the end result is that I have a PhD, and that is all that matters. That credential is not in doubt and not up for debate. Yes, I'm a scientist who isn't good at maths - we may be rare, but we do exist, so deal with it
So just accept that, and accept that my mathematical abilities are way below what you would consider to be the usual standard for a scientist. If you were to explain to me how something worked in qualitative, non-mathematical terms, then I could follow you and understand how the process worked. If you explain it to me in terms of an equation, then I have to spend a hell of a long time trying to figure out what is going on, and I probably wouldn't understand how it worked anyway. That doesn't make me less of a scientist, it just means that I have immense difficulty doing the mathematics and thinking quantitatively myself, if I can even do it at all.
Are we clear on this now?
Last edited by Evil Dr Ganymede on 27.05.2005, 23:54, edited 3 times in total.
Indeed, my equation could be simplified considerably. Sorry, I didn't took time to write it correctly. Here it is, but I can't confirm your equation was right, as I don't know the magnitude definition.
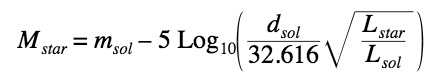
What is this damn number, 32.616 anywway ? Equations should always be writen in an unit independant way. Is this related to distance in parsecs ? I hate parsecs to death.
Edit : Okay, that stupid number is 10 parsecs, which means 32.616 LY.
I also found this web site :
http://www.astro.wesleyan.edu/~anna/Astro211/0326b.html
Does that helps ?
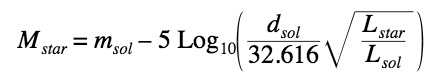
What is this damn number, 32.616 anywway ? Equations should always be writen in an unit independant way. Is this related to distance in parsecs ? I hate parsecs to death.
Edit : Okay, that stupid number is 10 parsecs, which means 32.616 LY.
I also found this web site :
http://www.astro.wesleyan.edu/~anna/Astro211/0326b.html
Does that helps ?
Last edited by Cham on 27.05.2005, 23:53, edited 1 time in total.
"Well! I've often seen a cat without a grin", thought Alice; "but a grin without a cat! It's the most curious thing I ever saw in all my life!"
-
Topic authorEvil Dr Ganymede
- Posts: 1386
- Joined: 06.06.2003
- With us: 21 years 8 months
Cham wrote:Indeed, my equation could be simplified considerably. Sorry, I didn't took time to write it correctly. Here it is, but I can't confirm your equation was right, as I don't know the magnitude definition.
What is this damn number, 32.616 anywway ? Equations should always be writen in an unit independant way. Is this related to distance in parsecs ? I hate parsecs to death.
32.616 is the number of lightyears in 10 parsecs. Yes, I think it's bloody annoying too. The Lsol is also irrelevant, since Lstar/Lsol is basically the luminosity of the star given in units of solar luminosity (i.e. if a star is twice the luminosity of Sol, then Lstar/Lsol = 2).
I think for your formula to make any sense though, that has to be d_star on top of the 32.616.
I'll give it a go and see if the numbers I get out of it make sense.

