Page 1 of 1
Moons orbiting inside of Double Giants?
Posted: 12.10.2004, 07:38
by Michael Kilderry
I am currently creating a double giant system and I have thought up the interesting idea of putting a moon that orbits around the center of gravity inside the orbits of the gas giants, and then I wondered, could this be possible in the real universe?
Michael Kilderry

Posted: 12.10.2004, 09:40
by revent
In a double system, the barycenter is going to be at the same place as the L1 point, and orbits around the L1 point are always unstable. Think about the gravitational pull as a potential field and you'll see why. When the moon is closer to one planet than the other, it wil no longer feel a net force toward the center of it's orbit (since one planet is closer) and it will proceed to enter a (probably EXTREMELY eccentric) orbit around the closer object.
Questions, Questions
Posted: 12.10.2004, 10:17
by Michael Kilderry
Wow!

That's interesting information. But is the world stable if it is right on the barycenter? Or will it be disrupted? Once it has entered that extremely eccentric orbit around one of the planets, will it then be stable? Or will the other planet steal it or fling it out of the planetary system altogether? Once in the new eccentric orbit, will the moon's orbit's perihelion be below the cloud layer of the gas giant or at least inside the roche limit to create a ring? Would it be an ECCENTRIC ring?
With my double giant system, I am still going to have the moon orbiting the barycenter. After all, this is one of the interesting things in a fictional system!

Michael Kilderry

Re: Questions, Questions
Posted: 12.10.2004, 16:47
by Evil Dr Ganymede
Michael Kilderry wrote:Wow!

That's interesting information. But is the world stable if it is right on the barycenter? Or will it be disrupted? Once it has entered that extremely eccentric orbit around one of the planets, will it then be stable? Or will the other planet steal it or fling it out of the planetary system altogether? Once in the new eccentric orbit, will the moon's orbit's perihelion be below the cloud layer of the gas giant or at least inside the roche limit to create a ring? Would it be an ECCENTRIC ring?
The L1 point is unstable. That means you can't get a world balanced right on it. Think of it as a hill with a point on the top - now try balancing a ball on it. You can't do it - the ball will always roll down the slope. You'd need to maintain the location using thrusters or something (which is how spacecraft stay there).
Certainly a world would never
form there. Something might push a satellite out to that point, and it's even possible that you could get it in a figure-of-eight orbit around the double giant (though I don't recall what configuration you need to have to get that to work), but I think it's more likely that the orbit would be unstable and it'd either collide with a planet or be flung out of the system.
I dunno about eccentric rings. I think if you're close enough to the planet to be within the roche limit, then the orbits of the ring particles would be very rapidly circularised by tides. It might be possible that the ring could be noticeably eccentric as it first forms though, but within a very short span of time (possibly as short as a few decades) it'd be circularised.
With my double giant system, I am still going to have the moon orbiting the barycenter. After all, this is one of the interesting things in a fictional system!

In that case, why are you asking about it in a Physics and Astronomy forum?

If you're not concerned with keeping it realistic, then you can do whatever you like - but in that case discussion of such a system strikes me as being rather out of place on this board.
Posted: 12.10.2004, 20:06
by tony873004
revent wrote:In a double system, the barycenter is going to be at the same place as the L1 point, and orbits around the L1 point are always unstable. Think about the gravitational pull as a potential field and you'll see why. When the moon is closer to one planet than the other, it wil no longer feel a net force toward the center of it's orbit (since one planet is closer) and it will proceed to enter a (probably EXTREMELY eccentric) orbit around the closer object.
You nailed it. That's exactly what would happen.
Even if the orbits of the gas giants were circular, making an object at the barycenter equidistant from them, it would still fall towards one or the other, like a ball on the top of the hill could start to roll in any direction.
Here's a test particle (blue) placed on the barycenter of 2 gas giants (300 earth masses each). The gas giants orbit their common barycenter in circular orbits 0.1 AU apart. The test particle hovers motionless at the barycenter for just a moment before deciding to fall into orbit around the red planet. Every time it passes through the barycenter region, it gives the green planet a chance to steal it from the red planet. The test particle switches from orbiting the red planet to orbiting the green planet and back again every few years.
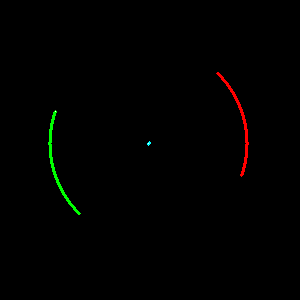

L1 != Barycenter.
Posted: 12.10.2004, 22:49
by wcomer
L1 and barycenter are two entirely different locations.
If they were the same, then the L1 of the earth moon system be beneath the earth's surface. And the Sun Earth barycenter closer to the earth than the sun.
Easy mistake to make, considering that in the special case of equal masses the two points would intersect.
Generally, the barycenter is not only not stable it is not a point of equilibrium.
Posted: 13.10.2004, 05:17
by Michael Kilderry
With my double giant system, I am still going to have the moon orbiting the barycenter. After all, this is one of the interesting things in a fictional system! - Michael Kilderry
In that case, why are you asking about it in a Physics and Astronomy forum? If you're not concerned with keeping it realistic, then you can do whatever you like - but in that case discussion of such a system strikes me as being rather out of place on this board. - Evil Dr Ganymede
I didn't put this this topic down because I wanted to make sure my solar system was realistic, I just put it down because I was just wondering if this was actually possible. It may sound a bit out of place, but even more out of place it'd be if I just put this one little paragraph down under a different section entirely! I think it still belongs in a certain section as long as the main point of the article is about the subject.
But thanks for your information though.
Michael Kilderry

Lagrange points
Posted: 20.11.2004, 02:12
by Ask H Larsen
I am no expert on astronomy, but you could place the planet on another Lagrange point and achieve a stable equilibrium. Does anyone know if this configuration is considered "probable" in dual systems?
Anyway, it involves a bit of mathematics to find the Lagrange points. I happen to have the numerical results for the Earth-moon system. Suppose we define a (right-angle) (x,y)-coordinate system such that the earth is at (0,0) and the moon at (1,0) at all times. Then the Lagrange points are:
[x, y]
1.1557, 0
0.8369, 0
-1.0051, 0
0.4879, 0.8660
0.4879, -0.8660
The last two points should be stable. They are (exactly)
(x,y) = (-µ+? , ? sqrt(3))
(x,y) = (-µ+? , -? sqrt(3))
where µ = mM/(m+M), where m and M are masses of the Moon and the Earth, and those equations should be general.
These calculations were made as part of a course in numerical analysis I had a few semesters ago.
Note that this model assumes that the object in the Lagrange point affects the surroundings only with negligible gravitational acceleration.
