Celestia Forums

Posted: **03.08.2004, 23:31**

Does anyone know a way to figure out the length of a day (where "day" here is the period from local sunrise to local sunset, not a day+night cycle) at a given latitude on a planet, given a rotation period for the planet and an axial tilt between 0 and 90 degrees (and possibly the length of the year too, since at 90 degrees presumably the length of a day is equal to half the orbital period?)?

Is there a handy simple formula for it, or is it horribly complex?!

Posted: **04.08.2004, 00:55**

There's more inputs needed. The eccentricity of your planet's orbit will have an effect. Earth's eccentricity causes sundials to run as much as 15 minutes fast during certain times of the year. So will the shape of your planet, specifically the magnitude of the equatorial buldge (although its not very significant). And the angular size of the parent star, because sunrise officially begins when the Sun's limb crosses the horizon, but the center is still below the horizon. Sunset is when the entire sun sets below the horizon. Then you'd have atmospheric refraction which might make the sun rise early and set late. Also, like you said, the length of the year is important. Earth spins every 23 hours and 56 minutes, but our day+night length is 4 minutes longer. The different orbital periods and different rotational periods will give you different results in this department.

I wrote a program once (using someone else's formulas) that computes sunrise and sunset for any place on Earth. The formulas that I borrowed from Astronomy for the Personal Computer were mind-boggling. I could show them to you if you want, but they're only for Earth. If I remember correctly, the code was about 100 lines long, but it took all those things into account.

I'm pretty sure that there is a simple formula if you're willing to treat this as a simple geometry and trigonometry problem, conceding that length of day is from "center of the sun" sunrise to "center of the sun" sunset, on an airless planet (to eliminate refraction) that was perfectly spherical in a perfectly round orbit. Then it should just be a simple SIN function with a few other things thrown in. I can probably come up with that for you if the simplified version will work for you.

Posted: **04.08.2004, 01:41**

erk. I figured as much...

I know there's a latitudinal effect and there's a seasonal effect too (I the longest day/shortest day is because of tilt, not eccentricity, right?). I'm not worried about the angular diameter of the star and the shape of the planet and refraction though, though the eccentricity would probably be worth factoring in...

Would that make it more manageable??

Posted: **04.08.2004, 12:46**

Evil Dr Ganymede wrote:I know there's a latitudinal effect and there's a seasonal effect too (I the longest day/shortest day is because of tilt, not eccentricity, right?).

Definitely the axial tilt is most important factor. Difference between day/night periods becomes dramatic especially in very north or south latitudes. Within the polar circles there are periods of no night at summer and no day at winter. At the poles day and night last half a year both (if eccentricity is not counted; actually in northern hemisphere summer lasts longer because Earth is near aphelion and vice versa).

I tried to calculate it by myself, but instead found this site. They don't look terribly complex calculations.

Posted: **04.08.2004, 12:56**

The simplest case would be a spherical planet in a circular orbit, no refraction, and treating the sun as a point source.
In that situation, you first of all need to identify latitudes within the polar circles (that is, lat > (90-tilt)), in which case the maximum daylight period and maximum nighttime duration for that latitude are equal to the solar rotation period of the planet - you have a midnight sun in summer, no sunrise in winter, and all possible daylight durations in between during the rest of the year.
At latitudes below the polar circles, the following equation applies:

MinDay = acos[tan(lat)/tan(90-tilt)]/180*D

where D is the solar rotation period (ie, the rotation period with respect to the parent star, rather than the sidereal period) and MinDay is the minumum daylight period for that latitude (ie, the duration of midwinter's day). All angles must be in degrees. From the symmetry of the situation, the maximum daylight period is just D-MinDay. So for the specified latitude you can have any daylight duration between MinDay and (D-MinDay), depending on the season.

Once you introduce eccentricity it's going to get messy, because you then need to specify the season of periastron - you'll get less variation in daylight duration if periastron occurs near an equinox, and more if it occurs near a solstice.

Grant

Posted: **04.08.2004, 15:11**

Grant, should that equation be:

MinDay = (acos[tan(lat)/tan(90-tilt)]/180)*D ?

D can be in hours or seconds or any other units of time, right?

Not sure what the Solar Rotation Period is... do you mean synodic period?

If I try that for 48N latitude (I think that's my current latitude) on Earth (23 degree tilt) I get a MinDay length of 8.25 hours, which means a Maxday of 15.75 hours. I can't find a place to check that though, but it sounds about right...

Ynjevi - thanks for the link. Though I think those do look rather complex!

Posted: **04.08.2004, 15:32**

Evil Dr Ganymede wrote:Grant, should that equation be:

MinDay = (acos[tan(lat)/tan(90-tilt)]/180)*D ?

Uh ... yes, if you like. Your extra brackets don't make any difference to the equation if you follow the conventional evaluation order.

Evil Dr Ganymede wrote:D can be in hours or seconds or any other units of time, right?

Yes. The bit you've put in brackets is simply the fraction of a solar day for which the surface is illuminated at solstice, so MinDay is expressed in whatever units you've used for D.

Evil Dr Ganymede wrote:Not sure what the Solar Rotation Period is... do you mean synodic period?

Mixing my terminology, sorry. Solar day or synodic period, yes.

Grant

Posted: **04.08.2004, 15:46**

granthutchison wrote:Uh ... yes, if you like. Your extra brackets don't make any difference to the equation if you follow the conventional evaluation order.

Well, at first I was reading that as "divide everything by (180*D)" which was making silly results.

One more thing...

In that situation, you first of all need to identify latitudes within the polar circles (that is, lat > (90-tilt)), in which case the maximum daylight period and maximum nighttime duration for that latitude are equal to the solar rotation period of the planet - you have a midnight sun in summer, no sunrise in winter, and all possible daylight durations in between during the rest of the year.

I'm not sure how things work above the polar circles - is there a way to figure out how long the midnight sun/no sunrise periods last as a fraction of a year?

Posted: **04.08.2004, 15:50**

Evil Dr Ganymede wrote:If I try that for 48N latitude (I think that's my current latitude) on Earth (23 degree tilt) I get a MinDay length of 8.25 hours, which means a Maxday of 15.75 hours. I can't find a place to check that though, but it sounds about right...

The sunrise and sunset calculator here gives a 15 hour 23 minute day on 21st July this year in Seattle, so we're in the ballpark. I'd hope that a more accurate value for latitude and tilt would move this a little closer to my equation.

Grant

Posted: **04.08.2004, 15:52**

Anonymous wrote:
Evil Dr Ganymede wrote:If I try that for 48N latitude (I think that's my current latitude) on Earth (23 degree tilt) I get a MinDay length of 8.25 hours, which means a Maxday of 15.75 hours. I can't find a place to check that though, but it sounds about right...
The sunrise and sunset calculator here gives a 15 hour 23 minute day on 21st July this year in Seattle, so we're in the ballpark. I'd hope that a more accurate value for latitude and tilt would move my equation a little closer to this value.

Grant

Posted: **04.08.2004, 15:54**

Bugger - got logged off and didn't notice. The second post (the one entirely in quotes), is what I meant to say in my first post. :oops:

Grant

Posted: **04.08.2004, 17:40**

I get better results with Grant's formula by comparing with data from http://www.srrb.noaa.gov/highlights/sun ... nrise.html
It only differed by a few minutes, which can be explained if their calculations don't use point mass and if refraction is included.

I suck at entering numbers into a calculator without making mistakes, so based on Grant's formula I made this: (I'll try to add a seasonal input later)

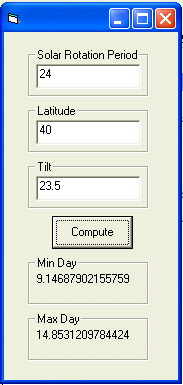
which you can get here:
http://orbitsimulator.com/celestia/Project1.exe

VB6 Source code:

Private Sub Command1_Click()
Dim tilt As Double, lat As Double, d As Double, maxday As Double

tilt = Radians(Val(txtTilt.Text))
lat = Radians(Val(txtLat.Text))
d = Val(txtRP.Text)

minday = (aCos(Tan(lat) / Tan(Radians(90) - tilt)) / Radians(180)) * d
maxday = d - minday

lblMin.Caption = minday
lblMax.Caption = maxday
End Sub

Function aCos(x As Double) As Double
aCos = Atn(-x / Sqr(-x * x + 1)) + 2 * Atn(1)
End Function

Function Radians(d As Double) As Double
Radians = (d / 180) * Atn(1) * 4
End Function

Posted: **04.08.2004, 17:58**

Hi Tony:
Nice calculator. Can I suggest:
1) Changing that first label to "Solar Day" to avoid perpetuating my dumb mixed terminology
2) Maybe trap the situation where lat > 90-tilt, and then force MinDay = 0 and MaxDay = d, to avoid crashing your cos function.

Grant

Posted: **04.08.2004, 18:37**

Oooh. Thanks, Tony. That's rather nifty

Posted: **04.08.2004, 20:00**

granthutchison wrote:Hi Tony:
Nice calculator. Can I suggest:
1) Changing that first label to "Solar Day" to avoid perpetuating my dumb mixed terminology
2) Maybe trap the situation where lat > 90-tilt, and then force MinDay = 0 and MaxDay = d, to avoid crashing your cos function.

Grant

Done!

Thanks Grant

New source:

Code: Select all

Private Sub Command1_Click()
Dim tilt As Double, lat As Double, d As Double, maxday As Double

tilt = Radians(Val(txtTilt.Text))
lat = Radians(Val(txtLat.Text))
d = Val(txtRP.Text)

If lat <= Radians(90) - tilt Then
    minday = (aCos(Tan(lat) / Tan(Radians(90) - tilt)) / Radians(180)) * d
    maxday = d - minday
Else
    minday = 0
    maxday = d
End If

lblMin.Caption = minday
lblMax.Caption = maxday
End Sub

Function aCos(x As Double) As Double
aCos = Atn(-x / Sqr(-x * x + 1)) + 2 * Atn(1)
End Function


Function Radians(d As Double) As Double
Radians = (d / 180) * Atn(1) * 4
End Function

Also, some of the difference between your formula and the sunset calculator page may also come because your formula is a round orbit formula. Earth's orbit is round enough for your formula to yield pretty good results, but when trying to explain away a few minutes it might make a small difference as well as the point source Sun and refraction.

By the way, the angular size of the sun makes only a small difference in equatorial and temperate latitudes, but can be quite significant at polar latitudes as the sun sets at a very shallow angle and lots of time can pass between first limb contact and full sunset.

What do you think about the seasonal input? Just my visual observations from San Francisco... The length of daylight seems to linger at the solstices, and speed through the equinoxes. The journey from minday to max day seems to be following a SIN curve (or COS depending on what you consider your starting point).

Evil Dr., just curious... What are you trying to do with the data? Habital locations?

Posted: **04.08.2004, 20:36**

Evil Dr Ganymede wrote:I'm not sure how things work above the polar circles - is there a way to figure out how long the midnight sun/no sunrise periods last as a fraction of a year?

Sorry, missed this post initially.
Yes, there's a very similar equation, using the same assumptions as previously. If lat > 90-tilt, then:

FullDaylight = acos[tan(90-lat)/tan(tilt)]/180 * Y

Y is the length of the year, in whatever units you like, and FullDaylight is the duration with either no sunset or no sunrise. This one begins to break down near the poles, where refraction and the non-zero angular diameter of the Sun mean that the "midnight sun" period is longer than calculated by my simple geometric equation, and the "polar night" period is shorter.

Grant

Posted: **04.08.2004, 21:18**

tony873004 wrote:The journey from minday to max day seems to be following a SIN curve (or COS depending on what you consider your starting point).

There's certainly a cosine involved:

Day = acos[cos(alpha)*tan(lat)/tan(90-tilt)]/180*D

where all assumptions are as before, Day is the duration of daylight, and alpha is the angular orbital distance from winter solstice. You can see that this is just the MinDay equation with cos(alpha) embedded in it.

Actually, it belatedly occurs to me that this calc can be streamlined as:

Day = acos[cos(alpha)*tan(lat)*tan(tilt)]/180*D

(You can apply similar tweakings to the other equations I've generated, based on the equality tan(x) = 1/tan(90-x).)

Grant

Posted: **05.08.2004, 01:06**

Your formulas seem to work quite well. Here's an updated calculator. The only thing it fails to do is compute day / night for artic regions that are not in their full daylight or full night period. I'll mess with that later.
http://orbitsimulator.com/celestia/Project1.exe

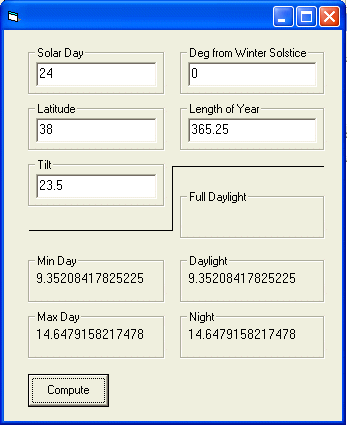
Code: Select all

Private Sub Command1_Click()
Dim tilt As Double, lat As Double, d As Double, maxday As Double
Dim Day As Double, Night As Double, FullDaylight, Y As Double, Alpha As Double
ClearLabels
tilt = Radians(Val(txtTilt.Text))
lat = Radians(Val(txtLat.Text))
d = Val(txtRP.Text)
Alpha = Radians(Val(txtAlpha.Text))
Y = Val(txtY.Text)
If lat <= Radians(90) - tilt Then
    minday = (aCos(Tan(lat) / Tan(Radians(90) - tilt)) / Radians(180)) * d
    maxday = d - minday
    Day = aCos(Cos(Alpha) * Tan(lat) * Tan(tilt)) / Radians(180) * d
    Night = d - Day
    lblDay.Caption = Day
    lblNight.Caption = Night
Else
    minday = 0
    maxday = d
    FullDaylight = aCos(Tan(Radians(90) - lat) / Tan(tilt)) / Radians(180) * Y
    lblFull.Caption = FullDaylight
End If

lblMin.Caption = minday
lblMax.Caption = maxday
End Sub

Function aCos(x As Double) As Double
aCos = Atn(-x / Sqr(-x * x + 1)) + 2 * Atn(1)
End Function

Function Radians(d As Double) As Double
Radians = (d / 180) * Atn(1) * 4
End Function

Sub ClearLabels()
lblMin.Caption = ""
lblMax.Caption = ""
lblDay.Caption = ""
lblNight.Caption = ""
lblFull.Caption = ""
End Sub

Posted: **05.08.2004, 09:46**

tony873004 wrote:Your formulas seem to work quite well.

Ah, high praise indeed :wink:

tony873004 wrote:The only thing it fails to do is compute day / night for artic regions that are not in their full daylight or full night period. I'll mess with that later.

The Day equation above should do that without modification. To avoid an acos crash, you could first evaluate the expression within the acos brackets of the Day equation: if it is >1 or <-1, branch to calculate FullDaylight; if it's a valid cosine, calculate Day.
(Sorry, you've probably got all that in mind already ... just thought I'd mention it.)

Grant

Posted: **05.08.2004, 17:45**

granthutchison wrote: The Day equation above should do that without modification. To avoid an acos crash, you could first evaluate the expression within the acos brackets of the Day equation: if it is >1 or <-1, branch to calculate FullDaylight; if it's a valid cosine, calculate Day.
(Sorry, you've probably got all that in mind already ... just thought I'd mention it.)

Grant

That's pretty much what I had in mind. Trapping it between -1 and 1 solved that problem.

http://orbitsimulator.com/celestia/Project1.exe

Code: Select all

Private Sub Command1_Click()
Dim tilt As Double, lat As Double, d As Double, maxday As Double
Dim Day As Double, Night As Double, FullDaylight, Y As Double, Alpha As Double
ClearLabels
tilt = Radians(Val(txtTilt.Text))
lat = Radians(Val(txtLat.Text))
d = Val(txtRP.Text)
Alpha = Radians(Val(txtAlpha.Text))
Y = Val(txtY.Text)
If lat <= Radians(90) - tilt Then
    minday = (aCos(Tan(lat) / Tan(Radians(90) - tilt)) / Radians(180)) * d
    maxday = d - minday
    Day = aCos(Cos(Alpha) * Tan(lat) * Tan(tilt)) / Radians(180) * d
    Night = d - Day
Else
    If Cos(Alpha) * Tan(lat) * Tan(tilt) > -1 And Cos(Alpha) * Tan(lat) * Tan(tilt) < 1 Then
        Day = aCos(Cos(Alpha) * Tan(lat) * Tan(tilt)) / Radians(180) * d
        Night = d - Day
    Else
        If Cos(Alpha) * Tan(lat) * Tan(tilt) < -1 Then
            Day = d
            Night = 0
        Else
            Day = 0
            Night = d
        End If
    End If
    minday = 0
    maxday = d
    FullDaylight = aCos(Tan(Radians(90) - lat) / Tan(tilt)) / Radians(180) * Y
    lblFull.Caption = FullDaylight
End If
lblDay.Caption = Day
lblNight.Caption = Night
lblMin.Caption = minday
lblMax.Caption = maxday
End Sub

Function aCos(x As Double) As Double
aCos = Atn(-x / Sqr(-x * x + 1)) + 2 * Atn(1)
End Function

Function Radians(d As Double) As Double
Radians = (d / 180) * Atn(1) * 4
End Function

Sub ClearLabels()
lblMin.Caption = ""
lblMax.Caption = ""
lblDay.Caption = ""
lblNight.Caption = ""
lblFull.Caption = ""
End Sub

[/code]

Celestia Forums

Day Length at high latitudes?

Day Length at high latitudes?