Orbit question

ajtribick · Post #1by **ajtribick** » 27.07.2005, 11:32

A question about orbits: suppose I have a planet orbiting its sun (planet mass ?‰? sun mass, so the sun stays fixed), with semimajor axis a, time period T, and eccentricity e. Given that at time t=0 the planet is at its maximum distance from the sun, what is its distance from the sun at some other time t?

Any help much appreciated, thanks.

Hamiltonian · Post #2by **Hamiltonian** » 27.07.2005, 15:52

It looks like all the equations you need to solve problems connecting times and positions in orbit are on this old thread - http://www.shatters.net/forum/viewtopic.php?t=3396, but for your problem (time -> obital position) you need to go backward through all the steps.

ajtribick · Post #3by **ajtribick** » 27.07.2005, 21:21

Thanks... why did I know this was going to involve solving transcendental equations.

M = E - e*sin(E)

I presume there's no easy shortcut, especially as I might want e>0.6627...

Spaceman Spiff · Post #4by **Spaceman Spiff** » 27.07.2005, 21:52

For such a high e there is definitely no easy way. You have to solve Kepler's equation iteratively for each E you want for each M, and you can only get a quick convergence starting with E = M when e < 0.1. For such a high e, you'll need to read off a good starting value from Kepler's graphs (which I can't post here...).

Either way, it's a job best done with a computer programme. Can you write one?

Ever wonder how Johannes Kepler felt about it?

Spiff.

tony873004 · Post #5by **tony873004** » 08.08.2005, 07:41

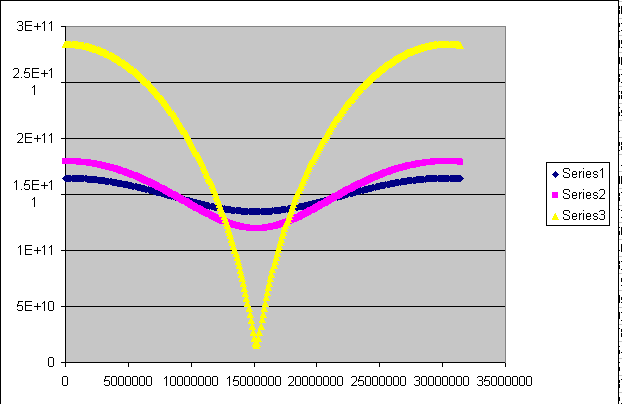
Here's a graph I put together using Gravity Simulator plotting distance (meters, y axis) vs. time (seconds, x axis). All 3 planets have a semi-major axis of 1 AU around a solar-mass object.

Series 1: ecc = 0.1
Series 2: ecc = 0.2
Series 3: ecc = 0.9

I don't know how to compute it, but there should be a nice simple formula to describe these plots without having to resort to numeric integration (computer method).