Can this be included in Celestia if it isn't there yet? I have a 2-D model that can be used to make a texture from an Earth'-based vantage point.
http://stevealbers.net/albers/allsky/outerspace.html (caption and additional images)
Then the next step would be a 3-D model including scattering.
Zodiacal Light
Zodiacal Light
http://stevealbers.net
Thanks john71. The 2-D version can perhaps be shown using the same procedure for displaying the Milky Way, or for the outer solar corona. In fact the zodiacal light is really a seamless extension of the corona. I presently have this as a FORTRAN subroutine that can be called to generate the 2-D brightness field.
The 3-D version would be similar to doing a galaxy fly through if this is presently possible.
The 3-D version would be similar to doing a galaxy fly through if this is presently possible.
http://stevealbers.net
-
Alexell
- Site Admin
- Posts: 303
- Joined: 07.10.2010
- Age: 31
- With us: 14 years 3 months
- Location: Moscow, Russia
- Contact:
Beautiful! And a great idea.
Added after 7 minutes 4 seconds:
https://github.com/CelestiaProject/Celestia/issues/8
Added after 7 minutes 4 seconds:
https://github.com/CelestiaProject/Celestia/issues/8
Admin of celestia.space
PC: Intel Core i7-8700 @ 3.20GHz, SSD, 16 Gb RAM, NVIDIA GeForce GTX 1080, Creative Sound Blaster ZxR. Windows 10 x64.
Phone: iPhone Xs 256 Gb. iOS 14.

PC: Intel Core i7-8700 @ 3.20GHz, SSD, 16 Gb RAM, NVIDIA GeForce GTX 1080, Creative Sound Blaster ZxR. Windows 10 x64.
Phone: iPhone Xs 256 Gb. iOS 14.

-
FarGetaNik
- Posts: 484
- Joined: 05.06.2012
- With us: 12 years 7 months
- Location: Germany
Here as a starting point is a quick cut-paste of some FORTRAN code for the zodiacal light that also includes a smooth version of the solar corona. An angular perturbation could be included for streamers. The 'vzod' result is the magnitudes per square arcsecond of the zodiacal light / corona, as seen from the vicinity of Earth. Other units can be derived such as spectral radiance and such.
-------------------------------------------------------------------------------------------------------------------------------
! Zodiacal Light S10 units 140 - 90 sin(beta) ecliptic latitude
elat = helioeclipticlat_a(ialt,jazi)
elon = helioeclipticlon_a(ialt,jazi)
if(elon .gt. 180.)elon = 360. - elon
s10zod_pole = 60. ! high ecliptic latitude
s10geg_ecliptic = 40. * cosd((elon-180.)/2.)**150.0
s10zod_ecliptic = 900. * cosd((elon)/2.0001)**7.7 + 140. + s10geg_ecliptic
! s10zod_ecliptic = 4000. * cosd((elon)/2.)**16.0 + 150. +
! s10geg_ecliptic
! Note the gegenschein of s10 = 40 can be added near
! helioecliptic 180.
eclp = 1.9 - 0.9*abs(elon/180.)
eclp = 1.0 ! control ecliptic sharpness
ecllatterm = abs(sind(elat))**eclp
s10zod = 10.**(log10(s10zod_pole) * ecllatterm + &
log10(s10zod_ecliptic) * (1.-ecllatterm))
! s10zod = (s10zod_pole) * ecllatterm + &
! (s10zod_ecliptic) * (1.-ecllatterm)
! s10zod = s10zod*10. ! debug for visibility
! F/K corona section (inner)
! http://arxiv.org/pdf/0909.1722.pdf (far corona in Fig 1.)
! https://ase.tufts.edu/cosmos/print_images.asp?id=28
! https://www.terrapub.co.jp/journals/EPS/pdf/5006_07/50060493.pdf
! "Interplanetary Dust" edited by B. Grun
sqarcsec_per_sqdeg = 3600.**2
size_glow_sqdg = 0.2 ! sun/moon area
delta_mag = log10(size_glow_sqdg*sqarcsec_per_sqdeg)*2.5
distr = sqrt(elat**2 + elon**2)
distr2 = max(distr,0.40) ! account for pixel size
srad = distr2/0.25
spowerk = 5.7 + srad * 2.0
spowerf = 7.5 + log10(srad) * 2.0
! spowerf = 8.0 + log10(srad) * 2.0
! spowerf2 = 8.3 + srad * 0.16
smag_eff = -26.7 + 2.5 * min(spowerk,spowerf)
rmag_per_sqarcsec = smag_eff + delta_mag
elong = min(sqrt(elon**2 + elat**2),180.)
coeff = 3.5 - 2.5*cosd(elong/2)**180.
if(elong .gt. 0.)then
! pcoeff = 1.0 - elon**2/(elon**2 + elat**2)
! pcoeff = abs(elat) / sqrt(elon**2 + elat**2)
! The last exponent controls ecliptic sharpness
pcoeff = (abs(elat) / sqrt(elon**2 + elat**2))**1.3
else
pcoeff = 0.
endif
fexp = -2.5*(1.-pcoeff) + (-2.8*pcoeff)
f_wm2srum = coeff * srad**fexp
f_s10 = wm2srum_to_s10(f_wm2srum)
! f_nl = wm2srum_to_nl(f_wm2srum)
! Merge original zodiacal light with corona
s10zod2 = max(s10zod,f_s10)
sbu = s10zod2 * 1.25
vzod = s10_to_magsecsq(s10zod2)
glow_zod = log10(v_to_b(vzod))
-------------------------------------------------------------------------------------------------------------------------------
! Zodiacal Light S10 units 140 - 90 sin(beta) ecliptic latitude
elat = helioeclipticlat_a(ialt,jazi)
elon = helioeclipticlon_a(ialt,jazi)
if(elon .gt. 180.)elon = 360. - elon
s10zod_pole = 60. ! high ecliptic latitude
s10geg_ecliptic = 40. * cosd((elon-180.)/2.)**150.0
s10zod_ecliptic = 900. * cosd((elon)/2.0001)**7.7 + 140. + s10geg_ecliptic
! s10zod_ecliptic = 4000. * cosd((elon)/2.)**16.0 + 150. +
! s10geg_ecliptic
! Note the gegenschein of s10 = 40 can be added near
! helioecliptic 180.
eclp = 1.9 - 0.9*abs(elon/180.)
eclp = 1.0 ! control ecliptic sharpness
ecllatterm = abs(sind(elat))**eclp
s10zod = 10.**(log10(s10zod_pole) * ecllatterm + &
log10(s10zod_ecliptic) * (1.-ecllatterm))
! s10zod = (s10zod_pole) * ecllatterm + &
! (s10zod_ecliptic) * (1.-ecllatterm)
! s10zod = s10zod*10. ! debug for visibility
! F/K corona section (inner)
! http://arxiv.org/pdf/0909.1722.pdf (far corona in Fig 1.)
! https://ase.tufts.edu/cosmos/print_images.asp?id=28
! https://www.terrapub.co.jp/journals/EPS/pdf/5006_07/50060493.pdf
! "Interplanetary Dust" edited by B. Grun
sqarcsec_per_sqdeg = 3600.**2
size_glow_sqdg = 0.2 ! sun/moon area
delta_mag = log10(size_glow_sqdg*sqarcsec_per_sqdeg)*2.5
distr = sqrt(elat**2 + elon**2)
distr2 = max(distr,0.40) ! account for pixel size
srad = distr2/0.25
spowerk = 5.7 + srad * 2.0
spowerf = 7.5 + log10(srad) * 2.0
! spowerf = 8.0 + log10(srad) * 2.0
! spowerf2 = 8.3 + srad * 0.16
smag_eff = -26.7 + 2.5 * min(spowerk,spowerf)
rmag_per_sqarcsec = smag_eff + delta_mag
elong = min(sqrt(elon**2 + elat**2),180.)
coeff = 3.5 - 2.5*cosd(elong/2)**180.
if(elong .gt. 0.)then
! pcoeff = 1.0 - elon**2/(elon**2 + elat**2)
! pcoeff = abs(elat) / sqrt(elon**2 + elat**2)
! The last exponent controls ecliptic sharpness
pcoeff = (abs(elat) / sqrt(elon**2 + elat**2))**1.3
else
pcoeff = 0.
endif
fexp = -2.5*(1.-pcoeff) + (-2.8*pcoeff)
f_wm2srum = coeff * srad**fexp
f_s10 = wm2srum_to_s10(f_wm2srum)
! f_nl = wm2srum_to_nl(f_wm2srum)
! Merge original zodiacal light with corona
s10zod2 = max(s10zod,f_s10)
sbu = s10zod2 * 1.25
vzod = s10_to_magsecsq(s10zod2)
glow_zod = log10(v_to_b(vzod))
http://stevealbers.net
As per some off-line discussions, the above code is related to constructing a 2-D brightness field for the zodiacal light. This may not be a texture per se, though it could be used to create one if needed. Otherwise it can be calculated dynamically. The tricky part is the equations are only valid for an observer on or near the Earth. A 3-D interplanetary dust model would be needed to see changes in the zodiacal light as we travel through the solar system. Nonetheless it can be a good start to only activate this for an observer near the Earth.
The 3-D model could be simple to start with, specifying dust concentration as a function of distance from the sun and ecliptic latitude. This could be adjusted to fit the observed zodiacal light seen from the Earth. I just found this reference about 3-D dust modeling:
http://cds.cern.ch/record/481511/files/0012033.pdf
The 3-D model could be simple to start with, specifying dust concentration as a function of distance from the sun and ecliptic latitude. This could be adjusted to fit the observed zodiacal light seen from the Earth. I just found this reference about 3-D dust modeling:
http://cds.cern.ch/record/481511/files/0012033.pdf
http://stevealbers.net
-
FarGetaNik
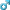
- Posts: 484
- Joined: 05.06.2012
- With us: 12 years 7 months
- Location: Germany
A 2D texture would be a nice start, it could simply fade out at higher distances. Celestia also suports 3D sprite models, but maybe it'll be hard to make it look smooth, not speckled. Smooth, fuzzy 3D model support opens many possibilites, like improved nebula and galaxy render, also benefiting Celestia. At least something to consider.
Here is a 2D texture for the zodiacal light and solar corona. The brightness range is saturating at both the high and low ends with an 8-bit image, so perhaps I should generate a 16-bit one? The coordinates are ecliptic latitude and longitude.
Note this can be used from the surface of the Earth or from near Earth orbit, or from space within a reasonable distance. The distance of the observer from the sun should be within around .9 to 1.1 AU and the distance from the ecliptic plane should be within roughly .03 AU. Outside of this envelope the 3-D dust is changing so we would need more of a 3-D dust model for rendering purposes.
Note this can be used from the surface of the Earth or from near Earth orbit, or from space within a reasonable distance. The distance of the observer from the sun should be within around .9 to 1.1 AU and the distance from the ecliptic plane should be within roughly .03 AU. Outside of this envelope the 3-D dust is changing so we would need more of a 3-D dust model for rendering purposes.
http://stevealbers.net
-
FarGetaNik
- Posts: 484
- Joined: 05.06.2012
- With us: 12 years 7 months
- Location: Germany
That's a good start, I think Celestia is capable of rendering such a texture already... Alexell posted an addon displaying the asteroid and Kuier Belts, if I remeber correctly it fades at certain ditances. It might be difficult to only display it at the intended range. Another possibility is to create a spherical Nebula... honestly I don't know how to implement it correctly at the moment.
For a texture it might be benificial to use 16 bit, or scaling the brightness with alpha. But the better solution certainly is to render 3D brightness distribution function.
For a texture it might be benificial to use 16 bit, or scaling the brightness with alpha. But the better solution certainly is to render 3D brightness distribution function.


