Celestia Forums

Most of this is greek to me. I'd like to construct this star system in Celestia. (It's actually a triple star.)

http://adsabs.harvard.edu/abs/2005MNRAS.356.1362D

http://esoads.eso.org/abs/2006A%26A...455..259A

Any help would be appreciated!

In fact, yes, it's more than enough information in as far as the primary pair goes. I'm not sure if there's enough for the secondary pair. If you want, I'll try and make up the .stc for it and post it here.

That,d be great! I'd love to see how the data is plugged in. In anticipation I'm digging thru SIMBAD now trying to find/ID the info I'd need to do the third star in the system. =)

I took the period, semi-major axis, and eccentricity from the paper, and just plugged it in. I used SIMBAD's measurement of distance though. You'll notice inclination, Ascending Node, Arg of Pericenter, and MeanAnomaly don't match the paper's. These values depend on the object's location in the sky. An object at the Celestial equator with i=90 would have i=0 in Celestia. It's just all how we define those attributes.

You have ARGofPericenter for BET Cen A at 318.16 and for BET Cen B at 138.16. Is that a typo or on purpose?

Slartibartfast wrote:You have ARGofPericenter for BET Cen A at 318.16 and for BET Cen B at 138.16. Is that a typo or on purpose?

Negative on being a typo. I took BET Cet A"s ArgOfPeri and subtracted 180. If I don't do this, the two stars will not function as a binary star. By subtracted half of 360, I rotate BET Cet B's orbit 180 degrees. In all binary systems, the shape of the orbit is the same. The only thing that changes is the size, and that one is rotated 180 degrees from the other.

Here's what I mean:
This is the Beta Centauri stars with identical orbital parameters for both stars.

As expected, the two stars have the exact same orbits, and even share the exact same position. This is atypical of most binary systems.

After we rotate the orbit of one of the stars by 180 degrees, (by adding or subtracting 180 to the ArgOfPeri), we get this:


This is far more representative of actual binary stars.

Slartibartfast wrote:I'd like to construct this star system in Celestia

I don't have any idea what you have in mind. If you want to do planets, it may be wise to position them around that third star you speak of, assuming it's in a wide orbit. As you can tell, BET Cen A and B are very close to each other, neither of them could hold a very stable planetary system, and for a system to be stable in a circumbinary orbit (in orbit of both stars from farther out) it would have to be a very wide orbit. Furthermore, Celestia doesn't yet allow for temperature computation of planets orbiting barycenters.

You want to talk about unstable orbit? The planet's supposed to be in the L4 of the third star. Can I construct the third star as if it were a planet? (I know that it is 110 AU out, orbiting them every 250 years. If there's a way to do it in the stc, that'd be even better of course. (It's a sci-fi planet moved to its orbit and kept there artificially, btw.)

BTW, how *do* you put a planet in the L4 of a star?

Slartibartfast wrote:You want to talk about unstable orbit? The planet's supposed to be in the L4 of the third star.

Interesting idea. The L4 and L5 points would constantly be shifting poitions due to the varying nature of the gravitational pull from the two central stars. So yeah, it would have to be kept there artifically.

Slartibarfast wrote:Can I construct the third star as if it were a planet?

Yeah, you sure can. To do such would require a slightly more complicated STC now. Now that we're adding in a third star, we're dealing with two barycenters. Based on

Slartibarfast wrote:I know that it is 110 AU out, orbiting them every 250 years

, I can make a rough STC, but much of the information will be either a guess, or unknown.

So, with a seperation of 110 AU, I'm arbitrarily giving the primary group 10 times the mass of the second group. The paper gives a mass of 9 solar masses for both BET Cen AA and BET Cen AB, amounting to 18 solar masses. I'm giving the arbitrary distance between BET Cen A to the BET Cen barycenter 10 AU, and the distance from BET Cen B to the BET Cen barycenter 100 AU. Thus, BET Cen B comes out to 1.8 solar masses. Now I don't know how accurate that is, and is, as so docmented, a guess.

Using


I get...

For putting the planet at L4 or L5, just put it out at the appropriate distance, give it the same orbital period as the orbital period of the star it orbits (250 years), and play with the ArgOfPericenter until it's in the right position.

Anyway, observe the structure of the STC file

-> Declare position of main barycenter.
-> Declare the second barycenter for AA and AB to orbit
-> Declare AA
-> Declare AB
-> Declare B

My planet is currently in a SSC file orbiting "Hadar". How do I change it to orbit the correct barycenter?

Slartibartfast wrote:My planet is currently in a SSC file orbiting "Hadar". How do I change it to orbit the correct barycenter?

If you make it orbit Hadar, it will probably orbit the main barycentre of the system. If you make it orbit "BET Cen B" then it will orbit the star you want.

I'm confused. =P Shouldn't it orbit the Hadar barycenter? So it can be in the L4 of the third star? If I put it around the third star (BET Cen B) then it won't be in the L4, it'll just be orbiting BET Cen B, right?

Also, to clear something up that's confusing.. you said you took the semimajor axis from the paper, but you have a value of 2.391 and the paper said 25.30. How did the latter number translate into the former?

Sorry to pester you with so many questions, but I can't learn if I don't ask, eh? Another question: you have the RA as 210.9558521, but everywhere I look in SIMBAD has a RA of 14 00 16.49 +/- some. How does the one number translate into the other? Also, you have the SIMBAD distance as 524.9597. I've spent the last hour or so combing SIMBAD for a distance and I seem to be too bloody ignorant to find one. Where should I look?

I hope these questions are at least mildly intelligent. (I've never had an astronomy course... my expertise is in history. =P )

Haha, nevermind about the RA question.... I figured it out! =) (I'm still stumped about the others tho.)

More data on the stars in question:

Star?€™s AA AB B
Spectral Class B1III B1III B8V
Luminosity 15,500(sun) 15,500(sun) 1,500(sun)
Mass 12.7(sun) 12.7(sun) 3.9(sun)
Diameter 8.2(sun) 8.2(sun) 3.15(sun)

(AA&AB may be B2III stars... info extracted from Jim Kaler's website plus formulae from Stephen's Gillett's "World Building").

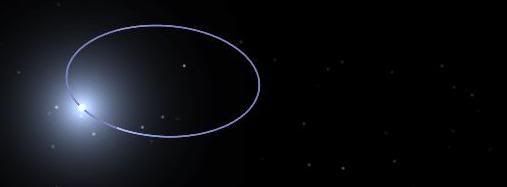
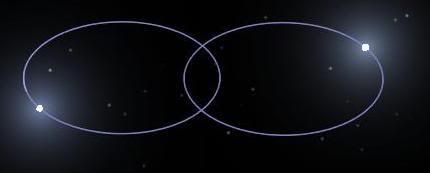
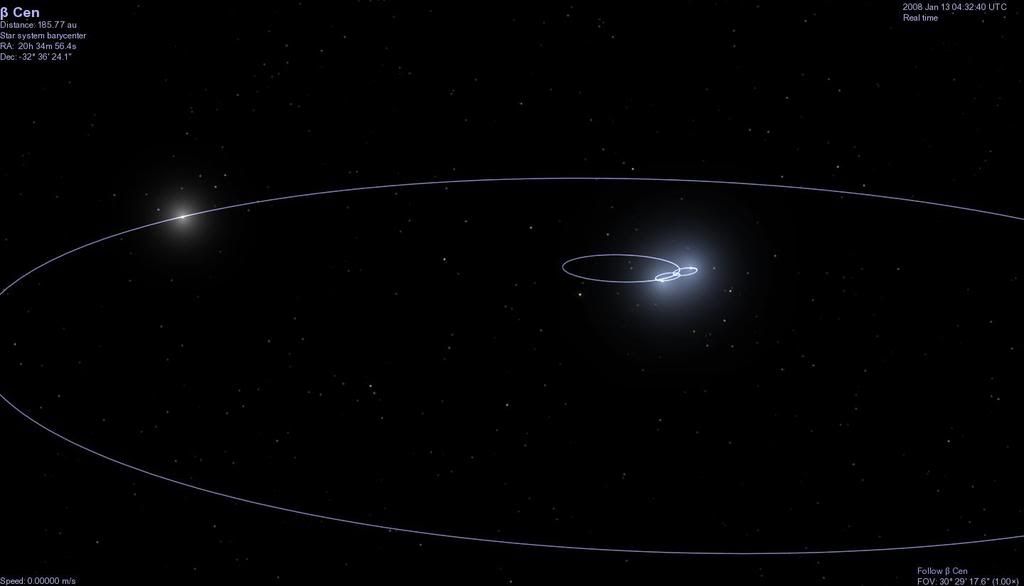
I apologize for the delay in answering, I had to go to sleep for the night X_X.

Slartibartfast wrote:I'm confused. =P Shouldn't it orbit the Hadar barycenter?

Yeah, you could probably do it that way too. That might be easier, lol.

Slartibartfast wrote:Also, to clear something up that's confusing.. you said you took the semimajor axis from the paper, but you have a value of 2.391 and the paper said 25.30. How did the latter number translate into the former?

The paper gives the semi-major axis in milliarcseconds (mas). This is a measurement of how much of the sky it occupies, rather than a physical size. So the true seperation would depend both on the 25.3 mas and the distance. Using an Excel sheet to do that math for me, I derrived 2.391 AU.

Slartibartfast wrote:Sorry to pester you with so many questions

It's quite alright, I don't mind.

Slartibartfast wrote:but I can't learn if I don't ask, eh?

Exactly.

Slartibartfast wrote:Also, you have the SIMBAD distance as 524.9597. I've spent the last hour or so combing SIMBAD for a distance and I seem to be too bloody ignorant to find one. Where should I look?

As the Earth moves in it's orbit around the sun, the apparent positions of the stars appear to change. This tiny amount of change is called the parallax. The higher the parallax, the more the stars appear to move, and the closer they are. To get distance from parallax, divide 1000 by the parallax (if it's in milliarcseconds, as it is in SIMBAD). This is your distance in parsecs. Now multiply that by 3.26 to get light years (alternatively, you can divide 3260 by the parallax to get light years).

Alright, with the new data you posted. The AB AA barycenter has a total mass of 25.4 solar masses, and B has a mass of 3.9 solar masses.

In any binary system, the distance between two objects (whether it be two stars, or a star and a barycenter, or two barycenters) is a ratio inversely equal to the ratio of their masses.

An object with 10 solar masses and an object with 1 solar mass are orbiting each other with a seperation of 11 AU. The 10 solar mass object will orbit 1 AU from the barycenter, and the 1 solar mass object will orbit 10 AU from the barycenter.

To solve for less, even, numbers, you can set it up like this.

x / y = 6.51282051282
x + y = 110

where x is the semi-major axis of the less massive star, and y is the semi-major axis of the more massive star. The more massive star or barycenter in this case, always has a smaller semi-major axis because it is not moved as much by the less massive star. You can solve this as any sort of system of equation.
Rearrange -> y=110 - x
Substitute -> x / (100 - x) = 6.51282051282

After solving, you should obtain 86.6894197952 AU for x.
Since x + y = 110, and x = 86.6894197952,
86.6894197952 + y = 100.
y = 23.3105802048 AU.

Updating the code with this information gives:


Post Scriptum: I'm rather bad at math, if anybody sees any mistake in my math, please point it out.

And now we have...

First a couple of minor questions. A.) How do you get it to show those happy, sparkly orbits of the stars? and 2.) Can you make that third star shine on a planet (ala specular power and all that shiny stuff.)

My next question is a bit more important. How do I make my planet orbit the barycenter? Below is what I have in the SSC for it.



I hope I quoted that code correctly. If I change "Hadar I" "Hadar" to "Hadar I" "BET Cen A" (or "BET Cen"), the planet disappears when I go to look at it in the program. Also, should I change the SemiMajoraxis to 86.6894197952 ? I know I need to tweak the Albedo again to get it to a habitable temperature.

The Regulus system is next on my docket. I'll use the data from the following URLs:

http://www.ari.uni-heidelberg.de/datenb ... c02615.htm
http://www.ari.uni-heidelberg.de/datenb ... c02616.htm
http://www.ari.uni-heidelberg.de/datenb ... c02617.htm
http://www.ari.uni-heidelberg.de/datenb ... c02618.htm

I may need help, but I'm going to do my best to do it on my own to show I've learned something at all from our chat. =) (It is much different data.. ex the orbit data is missing... but I think I might be able to find a work around.. the orbits take soooo long that I might be able to just ignore them... maybe?)